Tutorial

Boolean algebra has a system of different operators or logic gates which are known as "AND", "OR", and "NOT". These are the same gates that people will use in constructing computers. For each of the gates, there is always one output no matter how many inputs there are. This is not to be confused with a system of gates like the full adder or half adder.

We must be aware that Boolean algebra consists of only 1s or 0s, but this is not to be confused with binary numbers. Binary numbers can consist of multiple digits, but in Boolean algebra, there can only be a single digit per number. Furthermore, Boolean algebra is not like real math. In the end, there can only be the values of True or False. For example, in decimal or pretty much any basis of number, 1 + 1 = 2. However, in Boolean algebra, 1 + 1 = 1. A value greater than 1 or less than 0 cannot exist in Boolean algebra. In terms of addition, Boolean algebra will work like this. This is known as the OR gate.

0 + 0 = 0
0 + 1 = 1
1 + 1 = 1
1 + 1 = 1

Multiplication will also work in Boolean Algebra. Unlike addition, multiplication works just like multiplication for any other base. This is known as the AND gate.

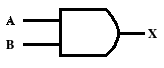
0 · 0 = 1
0 · 1 = 0
1 · 0 = 0
1 · 1 = 1

The values of "True" or "False" can also be converted to the opposite value. This function can be seen with the overline bar. This is known as the NOT gate.

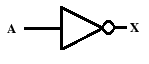
If A is false, A = 1
If A is true, A = 0

There's also one more gate we should be aware of. It's the XOR gate and you may see it in Boolean algebra. This gate should not be confused with the OR gate.

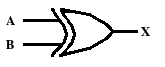
0 ⊕ 0 = 0
0 ⊕ 1 = 1
1 ⊕ 0 = 1
1 ⊕ 1 = 0

Below is a list of properties and laws that are used in Boolean algebra. Beside each law is a truth table that displays the possible outcomes.

Solving Simple Problems
Here are some examples of simple problems and the solutions.

• A + B + A
  Commutative Property: A + B = B + A
  = A + A + B
  Law of Tautology: A + A = A
  = A + B
   
• BCB
  Commutative Property: AB = BA
  = BBC
  Law of Complements: A · A = 0
  = 0 · C
  Law of Intersection: A · 0 = 0
  = 0
   
• C + 1 = B
  Law of Union: A + 1 = 1
  = 1 + B
  Law of Union: A + 1 = 1
  = 1
   
• X + Y + X
  Commutative Property: A + B = B + A
  = X + X + Y
  Law of Complements: A + A = 1
  = 1 + Y
  Law of Union: A + 1 = 1
  = 1

Using DeMorgan's Law
There are three steps to follow for using DeMorgan's Law while simplifying Boolean expressions.

1. Change all AND expressions to OR expressions, or vice versa.
2. Complement the individual terms that were ANDed or ORed.
3. Complement the whole expression.

Here is an example applied to A + B.

1. Change OR to AND.
    
   ⇒ A · B
    
2. Complement each term.
    
   ⇒ A · B
    
3. Complement the entire expression.
    
   ⇒ A · B

Here is an example of how DeMorgan's Law can be applied to an expression with two different solutions.

Solution I Solution II DeMorgan's Law on whole expression Commutative Property DeMorgan's Law on each expression Law of Tautology Associative Property DeMorgan's Law Commutative Property Law of Tautology

Complicated Problems
Here are some examples of complicated problems. Using your knowledge from previous examples, try to solve these problems below on your own.

• (A + B)(B + C)
  Distributive Property
  = B(A + C)
   
• AB C+ ABC + ABC + ABC
  Distributive Property
  AB(C + C) + BC(A + A)
  Laws of the Complements
  AB + BC
   
• (A + B + C)(A + B + C)
  Distributive Property
  (A + A)(B + C)
  Law of the Complements
  1(B + C)
  Law of Intersection
  B + C